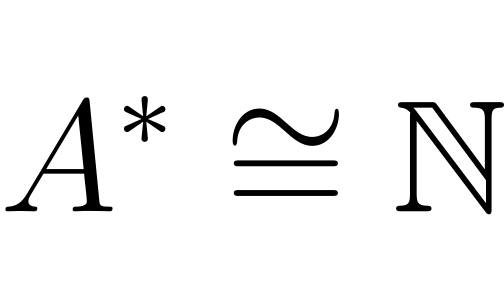How many words in a set of all words?

Motivation

I recently started a course called Languages and Automata, and because I am a math nerd I wanted to mathematically prove some things. But before I can even explain what I’m going to prove I need to introduce some other stuff. I just did this for fun and maybe this way I can get more accustomed to the course material or some other excuse to do this instead of making my homework.

Congruency

To figure out if two sets ($A$, $B$) are congruent we want to find some function $f: A \rightarrow B$ that is injective and surjective. Or, For all $x_1, x_2 \in A: f(x_1) = f(x_2) \Rightarrow x_1 = x_2$ (injective) and for all $b \in B$ there exists $a \in A$ so that $f(a) = b$ (surjective). So if we can find some function that is both injective and surjective (also called bijective) then we know that the sets $A$ and $B$ are congruent, noted as $A\cong B$.

Set of words

First we have alphabet, often denoted with $A$, they are a finite set of symbols. Examples are $A_1 = \{ a, b \}$, $A_2 = \{ A, C, G, T \}$ and $A_3 = \{if, then, while, …\}$. With an alphabet you can create a word (or string). For example, if $A=\{a, b\}$ then $abba$ and $ba$ are words. There is also the empty word that has no letters: $\lambda$. The set $A^*$ is a set made of all words in $A$.

Inductive definition of the set of words, $A^*$:

1. $\lambda \in A^*$.
2. If $x \in A$ and $v \in A^* $, then $xv \in A^*$.

Some notation:

• $|w|$ for the length of $w$: for instance $|aab|$ = 3.
• $|w|_a$ for the number of $a$’s in $w$: for instance $|aab|_a$ = 2.
• $w_i$ for the $i$-th letter of $w$: for instance $aab_2 = a$.

Proof

$A = \emptyset$

If $A = \emptyset$ then $A^* = \{\lambda\}$, which is just a finite set of one element, so there is not much to do here.

$A = \{a\}$

If $A = \{a\}$ then $A^* = \{\lambda, a, aa, aaa, …\}$ which is an infinite set. The bijective function for this one is pretty easy, simply take a function $f: \mathbb{N} \rightarrow A^*$ where $f(n) = a^n$. This is an injective function because if we take two numbers $a, b \in \mathbb{N}$. Then we take $w_a = f(a)$ and $w_b = f(b)$ if $w_a = w_b$ which means that both have the same number of a’s or that $a = b$.

Then we can make another function $g: A^* \rightarrow \mathbb{N}$ where $g(w) = |w|$, again this function is injective because we have an alphabet of only one letter.

And because we have two injective functions that go back and forth that means that there exists a bijective function between them and therefore:

\[A^* \cong \mathbb{N}\]

$|A| > 1$

First of all, the function $f$ that I previously defined is still injective in this case, but the function $g$ is not injective anymore as there are multiple words that get the same result: $g(aa) = g(bb)$ while, obviously, $aa \neq bb$. So we’ll have to create a new function $h: A^* \rightarrow \mathbb{N}$ that is injective. To do this I first want to define a new function $\iota: A \rightarrow \mathbb{N} - \{0\}$ that maps each letter to a number. Then we define the function $p: \mathbb{N} \rightarrow \mathbb{N}$ where $p(n)$ gives the $n$th prime. Then we define the function $h$ as:

\[h(w) = \prod_{i=1}^{|w|} p(i)^{\iota(w_i)}\]

How I came up with this function is that I thought about how to get unique numbers, well you can get it by multiplying primes, each number is a product of primes or a prime so if I can manage a unique prime decomposition for each word that function would be injective. By the Fundamental Theorem of Arithmetic (each number is either prime or a composite) if $h(w_1) = h(w_2)$ then the prime factorization of $h(w_1)$ and $h(w_2)$ are the same.

1. Matching word lengths: Because $h(w_1) = h(w_2)$ that means that the largest prime is the same, which means that the largest $p(i)$ is the same, which means that $|w_1| = |w_2|$.
2. Matching characters at each position: For each position $i$, the prime $p(i)$ in the product $h(w)$ is raised to the power $\iota(w_i)$. Let $w_1 = w_{1,1}w_{1,2}…w_{1,n}$ and $w_2 = w_{2,1}w_{2,2}…w_{2,n}$ then because $h(w_1) = h(w_2)$, it must be that $\iota(w_{1,i})=\iota(w_{2,i})$ for each $i=1,2,…,n$. Because $\iota$ is injective, this means that $w_{1,i}=w_{2,i}$ for each $i$.
3. Conclusion: Since $w_1$ and $w_2$ have the same length and the same characters at each position, it is easy to conclude that $w_1 = w_2$.

Conclusion

After all of that, it follows that:

\[A^* \cong \mathbb{N}\]

for any $A$ where $|A| \geq 1$.